leetcode | Leen'Blog

1 删除排序数组中的重复项

给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

示例 1:

给定数组 nums = [1,1,2], 

函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 

你不需要考虑数组中超出新长度后面的元素。

示例 2:

给定 nums = [0,0,1,1,1,2,2,3,3,4],

函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。

你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

个人解法

public class Solution {
    public int RemoveDuplicates(int[] nums) {
            if(nums.Length==0)
                return 0;
        int count=0;
        for(int i=1;i<nums.Length;i++){
            if(nums[count]!=nums[i]){
                
                nums[++count]=nums[i];
            }
        }
        return count+1;
    }
}

最佳
解法：双指针

首先注意数组是有序的，那么重复的元素一定会相邻。

要求删除重复元素，实际上就是将不重复的元素移到数组的左侧。

考虑用 2 个指针，一个在前记作 p，一个在后记作 q，算法流程如下：

1.比较 p 和 q 位置的元素是否相等。

如果相等，q 后移 1 位
如果不相等，将 q 位置的元素复制到 p+1 位置上，p 后移一位，q 后移 1 位
重复上述过程，直到 q 等于数组长度。

返回 p + 1，即为新数组长度。

画个图理解一下

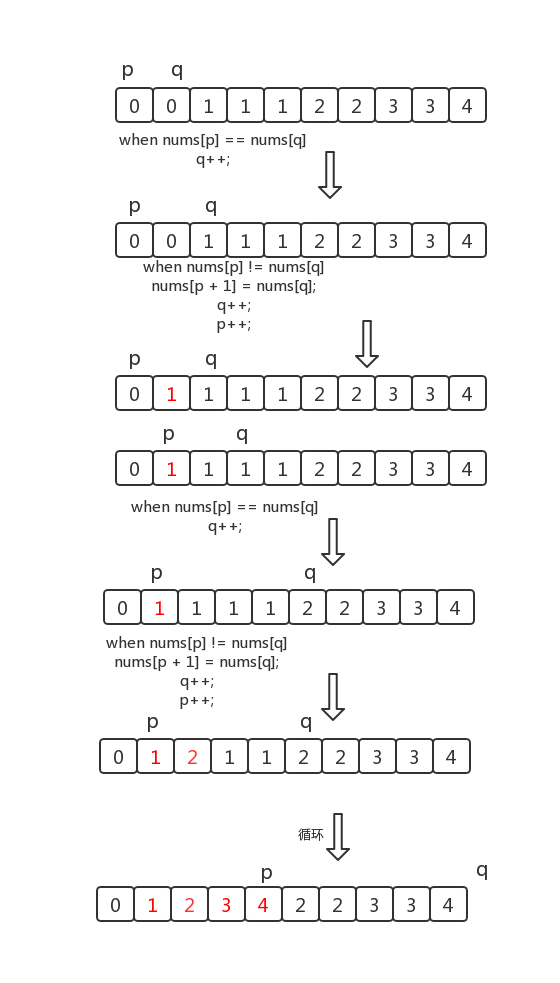
代码：


 public int removeDuplicates(int[] nums) {
    if(nums == null || nums.length == 0) return 0;
    int p = 0;
    int q = 1;
    while(q < nums.length){
        if(nums[p] != nums[q]){
            nums[p + 1] = nums[q];
            p++;
        }
        q++;
    }
    return p + 1;
}

复杂度分析：

时间复杂度：O(n)O(n)。
空间复杂度：O(1)O(1)。

优化：

这是大部分题解都没有提出的，在这里提一下。

考虑如下数组：

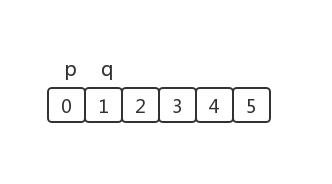
此时数组中没有重复元素，按照上面的方法，每次比较时 nums[p] 都不等于 nums[q]，因此就会将 q 指向的元素原地复制一遍，这个操作其实是不必要的。

因此我们可以添加一个小判断，当 q - p > 1 时，才进行复制。

代码：


public int removeDuplicates(int[] nums) {
    if(nums == null || nums.length == 0) return 0;
    int p = 0;
    int q = 1;
    while(q < nums.length){
        if(nums[p] != nums[q]){
            if(q - p > 1){
                nums[p + 1] = nums[q];
            }
            p++;
        }
        q++;
    }
    return p + 1;
}

复杂度分析：

时间复杂度：O(n)O(n)。
空间复杂度：O(1)O(1)。

2 移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1:

给定 nums = [3,2,2,3], val = 3,

函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。

你不需要考虑数组中超出新长度后面的元素。

示例 2:

给定 nums = [0,1,2,2,3,0,4,2], val = 2,

函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

注意这五个元素可为任意顺序。

你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

解法1

public class Solution {
    public int RemoveElement(int[] nums, int val) {
        int k=0;
        for(int i=nums.Length;i>0;i--){
            if(nums[i]!=val){
                nums[++k]=nums[i];
            }
        }
    }
}

解法2

public int removeElement(int[] nums, int val) {
    int i = 0;
    int n = nums.length;
    while (i < n) {
        if (nums[i] == val) {
            nums[i] = nums[n - 1];
            // reduce array size by one
            n--;
        } else {
            i++;
        }
    }
    return n;
}

6 加一

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1:

1
2
3

输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。

示例 2:

1
2
3

输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。

public class Solution
        {
            public int[] PlusOne(int[] digits)
            {
                Stack<int> myStack = new Stack<int>();
                bool isPlusOne = false;
                int length = digits.Length;
                for (int i = 0; i < length; i++)
                {
                    //数组最后一个元素，即遍历的第一个元素，不论何值都需要加1
                    if (i == 0)
                        isPlusOne = true;
                    
                    if (digits[length - 1 - i] == 9)
                    {
                        //对数组中为9的元素进行计算
                        int val = isPlusOne ? 0 : 9;
                        myStack.Push(val);
                        isPlusOne = val == 0 ? true : false;
                        continue;
                    }
                    else
                    {
                        //对数组中不为9的元素进行计算
                        int val = isPlusOne ? digits[length - 1 - i] + 1 : digits[length - 1 - i];
                        myStack.Push(val);
                        isPlusOne = false;
                        continue;
                    }
                }
                if (isPlusOne)
                    myStack.Push(1);
                //将栈中的元素存入数组
                int[] outArr = new int[myStack.Count];
                for (int i = 0; i < outArr.Length; i++)
                    outArr[i] = myStack.Pop();
                return outArr;
            }
        }

7.移动0

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

1 2	输入: [0,1,0,3,12] 输出: [1,3,12,0,0]

说明:

必须在原数组上操作，不能拷贝额外的数组。
尽量减少操作次数。

解法一个人解法

public class Solution {
    public void MoveZeroes(int[] nums) {
            int k=0;
            for(int i=0;i<nums.Length;i++){
                if(nums[i]==0){
                    k++;
                }else{
                    nums[i-k]=nums[i];
                }
            }
            for(;k>0;k--){
                nums[nums.Length-k]=0;
            }
    }
}

此解法将非零元素向前移动，记录零的个数最后补上零。

解法二

public class Solution {
    public void MoveZeroes(int[] nums) {
        if(nums==null||nums.Length==0)
        return;

        int k=0;
        for(int i=0;i<nums.Length;i++){
            if(nums[i]!=0){
                int tmp=nums[i];
                nums[i]=nums[k];
                nums[k++]=tmp;
            }
        }
    }
}

此解法参考快速排序的思想，快速排序首先要确定一个待分割的元素做中间点x，然后把所有小于等于x的元素放到x的左边，大于x的元素放到其右边。
这里我们可以用0当做这个中间点，把不等于0(注意题目没说不能有负数)的放到中间点的左边，等于0的放到其右边。
这的中间点就是0本身，所以实现起来比快速排序简单很多，我们使用两个指针i和j，只要nums[i]!=0，我们就交换nums[i]和nums[k]
//:#(作者：wang_ni_ma 链接：https://leetcode-cn.com/problems/move-zeroes/solution/dong-hua-yan-shi-283yi-dong-ling-by-wang_ni_ma/)

解法二的优化

public class Solution {
    public void MoveZeroes(int[] nums) {
        if(nums==null||nums.Length==0)
        return;

        int k=0;
        for(int i=0;i<nums.Length;i++){
            if(nums[i]!=0){
                if(i>k){
                int tmp=nums[i];
                nums[i]=nums[k];
                nums[k]=tmp;
                }
                k++;
            }
            
        }
    }
}

解法二当数组中零的个数较少时容易出现原地复制浪费资源，做个判断，当i与k指向的同一位置就不互换。

8两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

解法一个人解法

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        List<int> list=new List<int>();
        list.AddRange(nums);
        for(int i=0;i<nums.Length;i++){
            int tmp=target-nums[i];
            if(list.LastIndexOf(tmp)!=i&&list.Contains(tmp)){
                return new int[]{i,list.LastIndexOf(tmp)};
            }
        }
        return null;
    }
}

我想到了取差值但使用的List 实际上使用Hash比较方便

解法一优化

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
       Dictionary<int, int> dict = new Dictionary<int, int>();
        for(int i=0;i<nums.Length;i++){
            int tmp=target-nums[i];
            if(dict.ContainsKey(tmp)&&dict[tmp]!=i){
                return new int[]{i,dict[tmp]};
            }
            if(!dict.ContainsKey(nums[i]))
                dict.Add(nums[i],i);
        }
        return null;
    }
}

9数独

判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

上图是一个部分填充的有效的数独。

数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

示例 1:

输入:
[
[“5”,”3”,”.”,”.”,”7”,”.”,”.”,”.”,”.”],
[“6”,”.”,”.”,”1”,”9”,”5”,”.”,”.”,”.”],
[“.”,”9”,”8”,”.”,”.”,”.”,”.”,”6”,”.”],
[“8”,”.”,”.”,”.”,”6”,”.”,”.”,”.”,”3”],
[“4”,”.”,”.”,”8”,”.”,”3”,”.”,”.”,”1”],
[“7”,”.”,”.”,”.”,”2”,”.”,”.”,”.”,”6”],
[“.”,”6”,”.”,”.”,”.”,”.”,”2”,”8”,”.”],
[“.”,”.”,”.”,”4”,”1”,”9”,”.”,”.”,”5”],
[“.”,”.”,”.”,”.”,”8”,”.”,”.”,”7”,”9”]
]
输出: true
示例 2:

输入:
[
[“8”,”3”,”.”,”.”,”7”,”.”,”.”,”.”,”.”],
[“6”,”.”,”.”,”1”,”9”,”5”,”.”,”.”,”.”],
[“.”,”9”,”8”,”.”,”.”,”.”,”.”,”6”,”.”],
[“8”,”.”,”.”,”.”,”6”,”.”,”.”,”.”,”3”],
[“4”,”.”,”.”,”8”,”.”,”3”,”.”,”.”,”1”],
[“7”,”.”,”.”,”.”,”2”,”.”,”.”,”.”,”6”],
[“.”,”6”,”.”,”.”,”.”,”.”,”2”,”8”,”.”],
[“.”,”.”,”.”,”4”,”1”,”9”,”.”,”.”,”5”],
[“.”,”.”,”.”,”.”,”8”,”.”,”.”,”7”,”9”]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与示例1 相同。
但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
说明:

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
给定数独序列只包含数字 1-9 和字符 ‘.’ 。
给定数独永远是 9x9 形式的。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/valid-sudoku
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法一

public class Solution {
    public bool IsValidSudoku(char[][] board) {
           int[,] row=new int[9,10];
           int[,] col=new int[9,10];
           int[,] box=new int[9,10];
           for(int i=0;i<9;i++){
               for(int j=0;j<9;j++){
                   if(board[i][j]=='.')
                   continue;
                   int curNum=board[i][j]-'0';
                   if(row[i,curNum]==1 ||col[j,curNum]==1||box[j/3+(i/3)*3,curNum]==1 )
                   return false;
                   row[i,curNum]=1;
                   col[j,curNum]=1;
                   box[j/3+(i/3)*3,curNum]=1;
               }
           }
           return true;
    }
}

解法二
使用递归回溯正常情况下递归应该是比循环消耗更大，可该方法反而更快，没有找到原因。

class Solution {
    public boolean isValidSudoku(char[][] board) {
        if (board == null || board.length > 9 || board[0].length > 9 ) {
            return false;
        }

        return backTrace(board, 0, 0);
    }

    public boolean backTrace(char[][] board, int row, int col) {
        //如果col越界，那么重新指向下一行
        if (col == 9) {
            return backTrace(board,row+1,0);
        }
        //如果row越界，说明遍历完成，那么当前返回true
        if (row == 9) {
            return true;
        }

        //如果当前位置没有显示数字，直接跳向下一个位置
        if (board[row][col] == '.') {
            return backTrace(board,row,col+1);
        }
        // 这个位置数字已给出，需要试探，
        if (board[row][col] != '.') {
            //如果在当前位置上不成立直接返回false
            if (!isValid(board, row, col)) {
                return false;
            }
            //如果这个位置上成立。直接试探下一个位置
            return backTrace(board,row,col+1);
        }

        //如果全部遍历之后，没有false那么就返回true
        return true;
    }

    private boolean isValid(char[][] board, int row, int col) {
        char ch = board[row][col];
        // 三个方向，任一方向，其它8个位置上的数和当前位置ch不能相同
        for (int k = 0; k < 9; k++) {
            // 同一行九个位置已出现 ch
            if (board[row][k] == ch) {
                if (k != col) {
                    return false;
                }
            }
            // 同一列九个位置中已出现 ch
            if (board[k][col] == ch){
                if (k != row) {
                    return false;
                }
            }

            //看其他8个位置是否出现ch
            // 同一个子数独九个位置中已出现 ch
            if (board[(row / 3) * 3 + k / 3][(col / 3) * 3 + k % 3] == ch){
                if ((row / 3) * 3 + k / 3 != row && (col / 3) * 3 + k % 3 != col) {
                    return false;
                }
            }
        }
        return true;
    }
}

旋转图像

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

解法一
此解法不太普适，看到旋转后的行正好是旋转前列的倒置，以此规律，将每一列倒置后再变为行

var rotate = function(matrix) {
    var arr=[];
    for(let i=0; i<matrix.length;i++){
        let newCur=[];
        for(let j=0;j<matrix.length;j++){
            newCur.push(matrix[j][i]);
        }
        newCur.reverse();
        arr[i]=newCur;
    }

    for(let a=0;a<matrix.length;a++){
        for(let b=0;b<matrix.length;b++){
            matrix[a][b]=arr[a][b];
        }
    }
};

解法二
正规解法，按照坐标进行位置变换。

class Solution {
    public void rotate(int[][] matrix) {
        int temp;
        for (int x = 0, y = matrix[0].length - 1; x < y; x++, y--) {
            for (int s = x, e = y; s < y; s++, e--) {
                temp = matrix[x][s];
                matrix[x][s] = matrix[e][x];
                matrix[e][x] = matrix[y][e];
                matrix[y][e] = matrix[s][y];
                matrix[s][y] = temp;
            };
        };
    }
}

解法三
翻折法先上下翻折在沿副对角线翻折

class Solution {    
    public void rotate(int[][] matrix) {        
        int n = matrix.length;        
        //上下翻转        
        for (int i = 0; i < n / 2; i ++){            
            int[] tmp = matrix[i];            
            matrix[i] = matrix[n - i - 1];            
            matrix[n - i - 1] = tmp;       
        }        
        //对角线翻转        
        for (int i = 0; i < n; i ++){            
            for (int j= i + 1; j < n; j++){                
                int tmp = matrix[i][j];                
                matrix[i][j] = matrix[j][i];                
                matrix[j][i] = tmp;            
            }       
        }    
    }
}

在每一个数字中间加上一个“，”

知乎上的一个问题，如输入a[6]={1,2,3,4,5,6}输出1，2，3，4，5，6；
记录一个大佬的回答

#include <stdio.h>
int main(void){
    int a[6]={1,23,4,5,6};
    for(i=0;i<6;i++){
        printf(",%d"+!i,a[i]);
    }
    return 0;
}